Principio de Conexión Acausal
Parte 2
Dr. Adolfo R. Ordóñez
Introducción
Toda persona medianamente culta conoce cuán extraño y poco intuitivo (para el “sentido común”) es el comportamiento de la Naturaleza que describe la Física Cuántica. Recientemente este tema ha tenido gran difusión entre el público mundial con el filme -y luego el libro- “¿Y tú qué rayos sabes?”, referido a este tema.
Lo que es menos conocido es el asunto del “entrelazamiento
cuántico” (quantum entanglement). La descripción mecano-cuántica de un sistema
compuesto por muchas partículas –digamos de n partículas-, requiere de una
formulación holística, no reducible a un análisis de sus “partes”.
Traduciendo lo anterior al tema que estamos tratando, se
trataría de una posible explicación física de los eventos sincronísticos
descriptos –pero no “explicados”- por Jung. En el Cosmos todo está
entrelazado –y por ende “sincronizado” -con todo lo demás…
La Sincronicidad se debería a la existencia de correlaciones
no locales “a la Einstein-Podolsky-Rosen” (en adelante EPR) entre los astros y
la Naturaleza toda, los átomos y los seres vivientes.
Para decirlo en términos simples, la Mecánica Cuántica
predice que: Si dos partículas –cualesquiera, pero que por
simplicidad supondremos “gemelas”-interactuaron y luego se separan –por mucho
que sea-, pueden aún seguir “entrelazadas” y “compartiendo” algo que se llama
su “estado” o “función de onda”, algo así como un “paquete” matemático, el cual
contiene toda la información relevante que guía al sistema.
Y precisamente ese
hecho, hace que ambas, queden correlacionadas, o “sincronizadas” utilizando
terminología junguiana.
Estados cuánticos entrelazados y estados cuánticos no
entrelazados
 Por las leyes y propiedades cuánticas, cualquier medición
modifica a la función de onda Ψ t (se lee ‘Psi sub t’) del
sistema“total” formado por las dos partículas entrelazadas. Ello implica que si
alguien mide u “observa” un valor –digamos “s”- de una propiedad de una de
ellas –por ejemplo el espín [1], según una
dirección seleccionada para esa partícula- afecta al “estado” común del par, y
por ende, la otra partícula instantáneamente queda forzada a adoptar el valor
opuesto “-s”, justamente en la dirección elegida arbitrariamente para su
compañera ¿No es esto asombroso?
Por las leyes y propiedades cuánticas, cualquier medición
modifica a la función de onda Ψ t (se lee ‘Psi sub t’) del
sistema“total” formado por las dos partículas entrelazadas. Ello implica que si
alguien mide u “observa” un valor –digamos “s”- de una propiedad de una de
ellas –por ejemplo el espín [1], según una
dirección seleccionada para esa partícula- afecta al “estado” común del par, y
por ende, la otra partícula instantáneamente queda forzada a adoptar el valor
opuesto “-s”, justamente en la dirección elegida arbitrariamente para su
compañera ¿No es esto asombroso?(Aclaremos para quienes no vienen del ámbito fìsicomatemático que "espín"
 deriva de la palabra inglesa "spin", que proviene del verbo "to spin", o sea "girar", "rotar"; pues las partículas rotan además de desplazarse, como minúsculos "derviches" magnetizados. Hay partículas que cuando giran 180º, se las puede observar igual que si no hubieran rotado -como sucede con las Reinas del poker al girar en su plano alrededor de su centro-, y hay partículas que deben girar 360º para volver a quedar 'iguales' -como sucede con los humanos al girar alrededor de su columna vertebral-, pues si giramos sólo 180º nos verán de espaldas y no de frente. Y existen casos de "giros magnéticos" más complejos aún, hay partículas cuyo "giro" o espín se describe como siendo de 0, 1/2, 1, 3/2, 2,...)
deriva de la palabra inglesa "spin", que proviene del verbo "to spin", o sea "girar", "rotar"; pues las partículas rotan además de desplazarse, como minúsculos "derviches" magnetizados. Hay partículas que cuando giran 180º, se las puede observar igual que si no hubieran rotado -como sucede con las Reinas del poker al girar en su plano alrededor de su centro-, y hay partículas que deben girar 360º para volver a quedar 'iguales' -como sucede con los humanos al girar alrededor de su columna vertebral-, pues si giramos sólo 180º nos verán de espaldas y no de frente. Y existen casos de "giros magnéticos" más complejos aún, hay partículas cuyo "giro" o espín se describe como siendo de 0, 1/2, 1, 3/2, 2,...)
Supongamos un sistema cuántico “compuesto” –digámoslo así,
por ahora- de n partículas. Entonces, pueden ocurrir dos cosas:
- que la función de onda sea una sola función de todas las 3n variables, a saber, las 3n posibles posiciones según los tres ejes x, y, z de las n partículas de 1, 2, 3, 4, hasta n. En este caso, se dice que la única para el sistema considerado como un todo, es un estado cuántico “entrelazado”
- O bien, que haya n funciones de onda de 3 variables cada una, “separadas” y multiplicadas entre sí: En este caso no hay entrelazamiento cuántico, y se dice que se trata de n estados factorizados (o multiplicados), separados (o independientes entre sí), o desentrelazados
Lo que me interesa remarcar es que puede demostrarse que (en
un sentido matemático muy preciso) “hay muchos más” estados entrelazados que
factorizados. Ello implica que hay mucha más información debida a los
entrelazamientos de los sistemas “holísticos”, que la que se obtiene de
sistemas de partes independientes entre sí.
Más aún, si comenzamos con un sistema desentrelazado, –salvo
excepciones- su evolución temporal prescripta, según la cuántica, por la ecuación
de Schrödinger, lo sumergirá en un “mar de entrelazamientos” cada vez mayores.
Incluso tendríamos que admitir que, habiendo comenzado el Universo en un
Big-Bang a partir de un mismo “Punto”… ¡Ya debería estar todo entrelazado!
¿La Física Cuántica es válida sólo en el mundo microscópico?
Hasta hace poco se creía que sí. Hoy hay razones que nos
hacen suponer lo contrario.
La importantísima pregunta que se plantea Penrose en su libro
“El camino a la realidad” Cap. 23: ¿Qué significación tiene toda esa gigantesca
masa de información, que “no pareciera” estar presente en el mundo que nos es
observable, y donde siempre hemos creído que reina la “Física Clásica” –y no la
cuántica-?
Esto es una mera “creencia” sin una verdadera justificación,
así como la “suposición” de que la Física Cuántica reina casi
exclusivamente en el mundo microscópico, ya que -se supone- que en el mundo
macroscópico se produce una “decoherencia” que deshace toda posible acción
ondulatoria de importancia, y por ende alejando de nuestra percepción los
efectos típicos de la Cuántica, y dejando sólo los de la Física Clásica.  Por
supuesto, nunca se pudo dejar de considerar algunas notables “excepciones” como
los fenómenos que exhiben una manifiesta “coherencia”, tales como los de superfluidez
a muy bajas temperaturas, de superconducción, del rayo láser, etc. Sin embargo,
el formalismo matemático de David Bohm –que matemáticamente es equivalente al
de las otras interpretaciones de la cuántica- tiene la ventaja de hacer
transparente la falsedad de esas viejas suposiciones, tal como ha demostrado el
físico británico Peter Holland, de la Universidad de Bristol, en su libro de texto [2]. Por
otra parte, hoy se han acumulado muchos experimentos que demuestran la presencia
del accionar cuántico a nuestras temperaturas y en escalas macroscópicas, y no
meramente microscópicas.
Por
supuesto, nunca se pudo dejar de considerar algunas notables “excepciones” como
los fenómenos que exhiben una manifiesta “coherencia”, tales como los de superfluidez
a muy bajas temperaturas, de superconducción, del rayo láser, etc. Sin embargo,
el formalismo matemático de David Bohm –que matemáticamente es equivalente al
de las otras interpretaciones de la cuántica- tiene la ventaja de hacer
transparente la falsedad de esas viejas suposiciones, tal como ha demostrado el
físico británico Peter Holland, de la Universidad de Bristol, en su libro de texto [2]. Por
otra parte, hoy se han acumulado muchos experimentos que demuestran la presencia
del accionar cuántico a nuestras temperaturas y en escalas macroscópicas, y no
meramente microscópicas.
 Por
supuesto, nunca se pudo dejar de considerar algunas notables “excepciones” como
los fenómenos que exhiben una manifiesta “coherencia”, tales como los de superfluidez
a muy bajas temperaturas, de superconducción, del rayo láser, etc. Sin embargo,
el formalismo matemático de David Bohm –que matemáticamente es equivalente al
de las otras interpretaciones de la cuántica- tiene la ventaja de hacer
transparente la falsedad de esas viejas suposiciones, tal como ha demostrado el
físico británico Peter Holland, de la Universidad de Bristol, en su libro de texto [2]. Por
otra parte, hoy se han acumulado muchos experimentos que demuestran la presencia
del accionar cuántico a nuestras temperaturas y en escalas macroscópicas, y no
meramente microscópicas.
Por
supuesto, nunca se pudo dejar de considerar algunas notables “excepciones” como
los fenómenos que exhiben una manifiesta “coherencia”, tales como los de superfluidez
a muy bajas temperaturas, de superconducción, del rayo láser, etc. Sin embargo,
el formalismo matemático de David Bohm –que matemáticamente es equivalente al
de las otras interpretaciones de la cuántica- tiene la ventaja de hacer
transparente la falsedad de esas viejas suposiciones, tal como ha demostrado el
físico británico Peter Holland, de la Universidad de Bristol, en su libro de texto [2]. Por
otra parte, hoy se han acumulado muchos experimentos que demuestran la presencia
del accionar cuántico a nuestras temperaturas y en escalas macroscópicas, y no
meramente microscópicas.
Física Cuántica, sincronicidad y ‘no separabilidad
adentro/afuera’
De hecho, lo anterior, justifica nuestra convicción, de que:
El gran exceso de información de los “entrelazamientos
cuánticos” –mencionado por Roger Penrose- que “no parece evidente en nuestra
experiencia cotidiana”, es justamente lo que posibilita la base de una explicación
físico-matemática de los fenómenos de la Sincronicidad (vistos y descritos por
la mirada atenta y desprejuiciada de Carl Jung), y de la No Separabilidad
“adentro-afuera”, entre nosotros y el cosmos, (lo cual puede conferir una
“entrada científica” a la Astrología). Porque no solamente somos “polvo de
estrellas”, como decía Carl Sagan, sino que somos “polvo cuántico entrelazado”
de –y con las- estrellas.
Como los efectos de la “no localidad” cuántica -como el de
las dos partículas entrelazadas- pueden
parecer inentendibles y casi “mágicos”, Bohm ideó una forma de acercarlos más a la “lógica” de la realidad a la cual estamos acostumbrados. Daremos un ejemplo que describe muy gráficamente lo que ocurre [3].
Imaginemos que hay un “único” pez “tridimensional” (ya veremos para qué hacemos esta obvia aclaración) nadando en una pecera, el cual está siendo filmado por dos cámaras y , ubicadas paralelamente al piso y formando un ángulo de 180° entre sí. Además, supongamos que ambas filmaciones están siendo transmitidas a dos pantallas de televisión “bidimensionales” situadas una al lado de la otra, pero en un salón donde no es visible la pecera. Claramente, quienquiera que observe ambas imágenes, primero pensará que se trata de peces distintos. Así, como las cámaras enfocan al pez desde diferentes ángulos, si una de ellas muestra al pez de frente; la otra pantalla lo dejará ver de cola, y recíprocamente. Pero al cabo de observar las dos imágenes durante un rato, el observador se dará cuenta que amabas proyecciones están fuertemente correlacionadas. En efecto, a cualquier ángulo de observación que filme al pez una de las cámaras, le corresponderá el ángulo opuesto en la otra ¿Por qué razón?
parecer inentendibles y casi “mágicos”, Bohm ideó una forma de acercarlos más a la “lógica” de la realidad a la cual estamos acostumbrados. Daremos un ejemplo que describe muy gráficamente lo que ocurre [3].
Imaginemos que hay un “único” pez “tridimensional” (ya veremos para qué hacemos esta obvia aclaración) nadando en una pecera, el cual está siendo filmado por dos cámaras y , ubicadas paralelamente al piso y formando un ángulo de 180° entre sí. Además, supongamos que ambas filmaciones están siendo transmitidas a dos pantallas de televisión “bidimensionales” situadas una al lado de la otra, pero en un salón donde no es visible la pecera. Claramente, quienquiera que observe ambas imágenes, primero pensará que se trata de peces distintos. Así, como las cámaras enfocan al pez desde diferentes ángulos, si una de ellas muestra al pez de frente; la otra pantalla lo dejará ver de cola, y recíprocamente. Pero al cabo de observar las dos imágenes durante un rato, el observador se dará cuenta que amabas proyecciones están fuertemente correlacionadas. En efecto, a cualquier ángulo de observación que filme al pez una de las cámaras, le corresponderá el ángulo opuesto en la otra ¿Por qué razón?
Pues se trata de dos vistas “bidimensionales” distintas de
un único y mismo pez “tridimensional” (En la figura de más arriba, se ha tomado un ángulo de 90º -en vez de 180º- entre ambas cámaras; y en la de la izquierda, hemos reemplazado al pez por un cilindro, al ángulo de 180° por uno de 90°, y mostramos las dos proyecciones planas del cilindro: un cuadrado y un círculo, pero la idea es la misma; si imaginan mover al pez de arriba o al cilindro de la izquierda, variarán sus proyecciones bidimensionales "separadamente", pero ambas estarán claramente correlacionadas por ser proyecciones de un único ente de más dimensiones, en este caso tres).
Análogamente al ejemplo del “pez”, nuestras dos partículas
cuánticamente entrelazadas constituyen una única entidad multidimensional ψ
“psi” –una función de ondas- en un espacio de seis dimensiones, que Bohm nos
propone considerar tan “real” como un pez tridimensional. Y cada observación de
una de las dos partículas ya “separadas”, digamos la partícula “1” (o la “2”)
muestra una proyección de “la” función de ondas sobre las tres dimensiones del
espacio ordinario calculada en el punto donde se
halla ubicada “1” (o “2”, respectivamente). Ambas proyecciones “separadas”,
-que es todo lo que “vemos” del único e “inseparable” pez- están
correlacionadas, del mismo modo que en el ejemplo antes señalado: pues una muestra
la proyección “de frente” del pez (el valor “s”), y la otra la proyección “de
cola” (el valor “-s”) del mismo pez.
Dr. Adolfo R. Ordóñez
[1] El espín de una partícula es una propiedad cuántica que
hace que tenga un “momento magnético”, como si la partícula tuviera un “imán
subatómico”, pero con unos valores de “imantación” que están “dosificados” en múltiplos enteros de una mínima cantidad, y no
pueden, por ende, variar con continuidad por todos los valores intermedios. Acá son sólo dos: “s” y “-s” en cada dirección. Ver también más
adelante, cuando mencionemos a Wolfgang Pauli
[2] “The Quantum Theory
of Motion, an account of the Broglie-Bohm causal interpretation of quantum
mechanics”, Cambridge University Press.
[3] Ver por ejemplo:
John Briggs y David Peat “A través del maravilloso espejo del universo” (La
nueva revolución en la física, matemática, química, biología y neurofisiología
que conduce a la naciente ciencia de la totalidad); Gedisa editorial, Barcelona
1989, págs. 132-136.



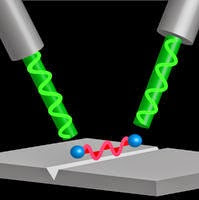





En el actual artículo Adolfo establece correlaciones entre la Física Cuántica y el Principio de la Sincronicidad
ResponderEliminar